- Os bucles.
- Teoría e Historia da Computación.
- Ordenador ou folla de cadriños (versión hard).
- Visualizando os bucles e anticipando o seguinte bucle.
- Con retos, intentando crear novos patróns.
- Pode aprender a programarse.
O xogo da vida foi creado por J.H. Conway en 1970 e forma parte dos chamados autómatas celulares, unha ferramenta importante na Historia da Computación (entre outras cousas foron descubertos por Von Neumann, celebre matemático, impulsor do primeiro ordenador), pero tamén en ramas das Matemáticas, Bioloxía ou Economía. A nivel computacional é moito máis que un xogo, e unha máquina de Turing (isto quere decir que pode computar calquera problema que poida ser computable!), e isto é razón máis que de sobra para coñecelo. Nunca serás unha programadora (ou programador) seria se non xogas, ou cando menos se non o programas ;-)
O primeiro que chama a atención é que é un xogo para 0 xogadores. Isto que significa?. Pois que no xogo a persoa tan só decide as condicións iniciais da partida, e logo deixa que evolucione automaticamente a partida para observar o resultado, que será altamente impredicible. O xogo terá gracia na medida que intentemos anticipar o resultado final, e que busquemos obter diferentes resultados.
A mecánica do xogo é a seguinte:
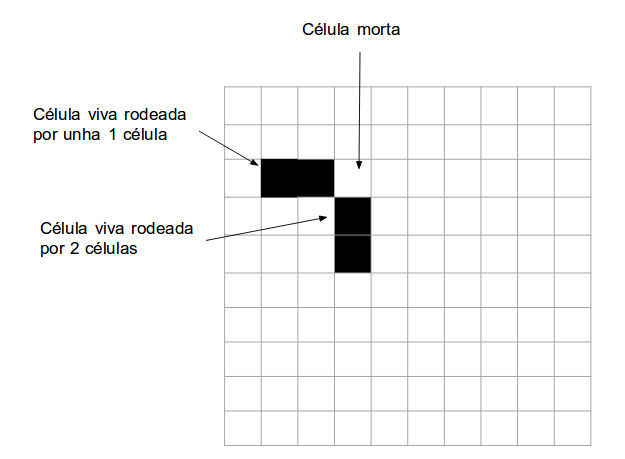
- Temos un escenario, unha grella infinita, en que cada cadriño é unha célula que pode estar viva (pintando de negro, por exemplo) ou morta (branco). En clase sen ordenador podemos usar unha folla de cadriños.
- Debuxamos un patrón, escollendo cadriños que son as células inicialmente vivas, e observamos como evolucionan no tempo. O tempo se marca en ciclos ou bucles.
- Cada celula viva se considera que está rodeada doutras células vivas se está en contacto horizontal, vertical ou diagonal (ou sexa, podería estar rodeada por 8 células).
- A evolución da partida ven marcada polas seguintes normas para cada ciclo:
- Unha célula morta (branca) que estea rodeada por exactamente 3 células vivas, nace no seguinte ciclo (pasa a ser negra).
- Unha célula viva rodeada de 2 ou 3 células vivas segue a estar viva no ciclo seguinte; en calquera outro caso morre (por exemplo, se só ten unha célula ao lado ou se ten catro).
- No seguinte ciclo ten cambiado o patrón de células vivas e mortas.
Que acontecerá co teu patrón ao longo do tempo, cando pasen bastantes ciclos?. Pois cousas moi diversas e imprevisibles:
| Nome do patrón |
Comportamento ao longo do tempo |
Exemplo |
|---|---|---|
| Extinto | Todas mortas. Dalgunha maneira é como se perderas, volve a empezar. |

|
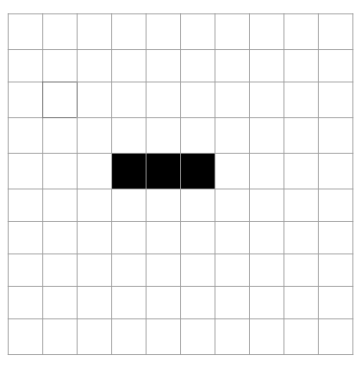
| Oscilador | Volve ao estado inicial. O máis sinxelo posible é o Blinker. |
|
| Estático | Repite o mesmo patrón. Pode ser de inicio ou ao cabo de varios ciclos. |

|
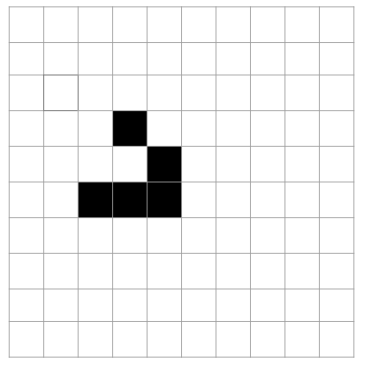
| Nave volante | Desprazase polo escenario. |
|
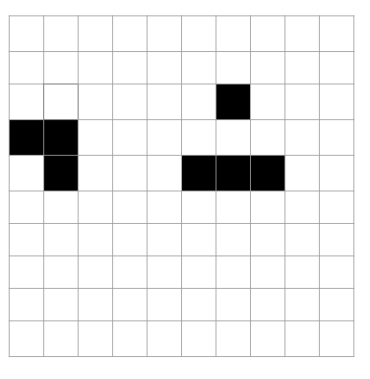
| Matusalén | Tarda moito en estabilizarse. |
|
E temos moitísimos máis: patróns que se moven e deixan rastro, patróns estáticos que envían naves...e por sorprendente que pareza poden facerse portas lóxicas, sumadores, xeradores de números primos...
| Patrón | Comportamento |
 Isto é unha "Pistola de planeadores de Gosper" (Gosper Glider Gun) |
 |
Se queres xogar agora mesmo podes facelo aquí embaixo. A parte de probar ao chou é interesante marcarse retos (osciladores, naves...) e buscar patróns xa feitos.
XOGO DA VIDA ONLINE: Gamoliyas
Existen moitas versións distintas do Xogo da Vida, e tamén xogos similares como a Formiga de Langton.
Cubo de Rubik Moon 1110011 Pedra_papel_tesoira Robodrez Xogo da vida