1. Función para binarizar un número
- Temos moitos xeitos de facelo. Neste caso será por divisións sucesivas.
- En Python temos unha función predefinida para facelo directamente (ou sexa, que nos gusta perder o tempo)
- Bucle namentres (repetir ata en Scratch) para pasos sucesivos.
- Variables: unha para o decimal, outra para almacenar 1 e 0 do binario (serán cadeas).
- Dividimos o número decimal entre 2 sucesivamente e almacenamos o resto na variable binaria.
Solución proposta (lembra, non é única):
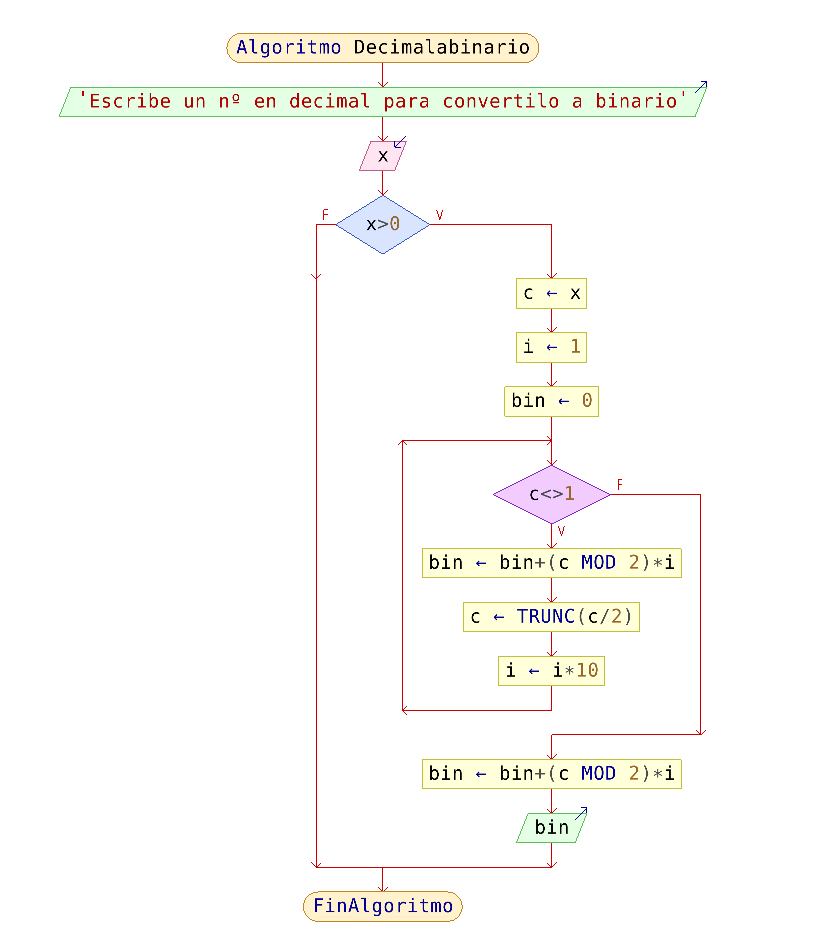
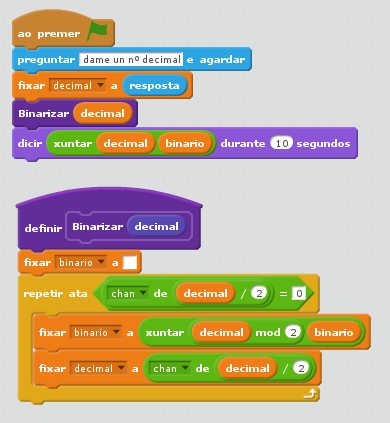
| Diagrama de fluxo (Pseint) | Scratch |
|
|
[Scratch:Uso de funcións: binarizar]
|
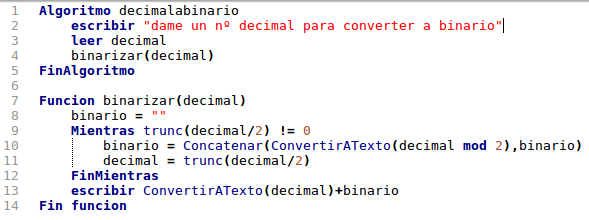
| Pseudocódigo (Pseint) | Python 3 |
|
|
|
[Repl.it: Binarizar]
- Busca a función de Python que permita facer o cálculo directamente.
- Engade unha opción para que se introducimos un número negativo ou unha cadea nos de erro e nos permita volver escribir o número.
2. Pasar de decimal a calquera base menor que 10
Fai unha función para calquera base menor de 10 (pasar de decimal a octal). Para iso terás que modificar a función anterior para que vaia dividindo o número entre 3, 4, 5.. ou a base que escollas. O resultado tería que ser así:

Engádelle a opción de sinalar o erro se o número é negativo ou se a base escollida é maior que 9.
3. Pasar de decimal a hexadedimal
O código hexadecimal ten moita importancia nas ciencias da computación, como xa vimos no apartado Como contan os ordendores. Como no noso sistema de numeración só temos 10 símbolos, para contar en hexadecimal deberemos facer man doutros 6 símbolos: as primeiras letras do alfabeto, de tal xeito que a partir do 9 contaremos como se amosa na táboa da dereita.
|
Hexadecimal
|
Decimal
|
|---|---|
|
A
|
10
|
|
B
|
11
|
|
C
|
12
|
|
D
|
13
|
|
E
|
14
|
|
F
|
15
|
Calquera número menor de 256 pódese escribir como a suma de dous díxitos en hexadecimal. Por exemplo:
| Decimal | Descomposición | Hexadecimal |
|---|---|---|
| 200 | 12 · 161+8 · 160 | C8 |
| 154 | 9 · 161+10 · 160 | 9A |
Escribe o programa en Python, creando unha función que converta de hexadecimal menor que 256 a decimal. Como na imaxe que se presenta a continuación co pseudocódigo do programa, crea unha lista para asignar a cada valor hexadecimal o seu símbolo.
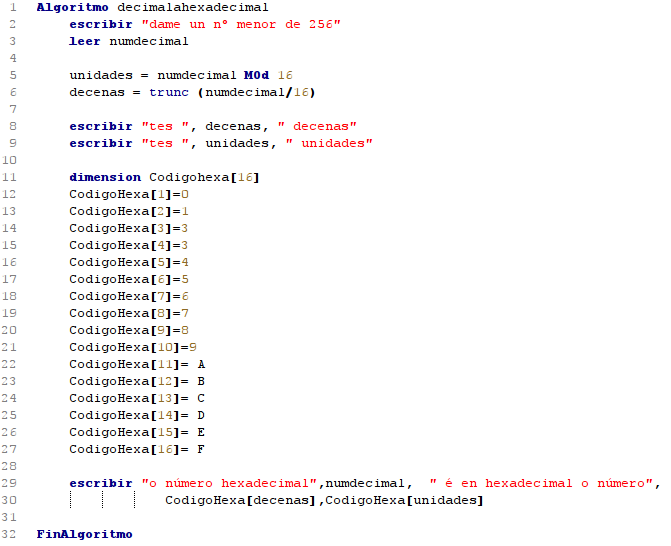
4. Pasar de hexadecimal a decimal.
Para pasar de hexadecimal a decimal haberá que facer a operación inversa. Vexamos un par de exemplos:
| Hexadecimal | Descomposición | Decimal |
|---|---|---|
| 174F | 1 · 163+7 · 162+4 · 161+15 · 160 | 5967 |
| ACDC | 10 · 163+12 · 162+13 · 161+12 · 160 |
44252 |
Deseña un programa en Python que faga esta conversión, definindo unha función.
5. Pasar de decimal a hexadecimal de 4 díxitos
Cos pasos explicados antes xa estas en disposición de exprimir o miolo e facer un programa que pasa de decimal a hexadecimal números menores que 65536 (é dicir números de catro díxitos hexadecimais).
6. Calculadora conversora
Con todas as funcións deste capítulo crea unha calculadora conversora entre decimal, binario e hexadecimal.
Binarizar e outras conversións Ordena e funcionará Máis orde Que ordene Python