Como contan os ordenadores (hardware)
Aínda que non se teña enterado moito profesorado de Matemáticas e de Informática, o ćodigo binario só é útil para electrónica dixital, non para programación. O que realmente utilizan os programadores é código hexadecimal (e outros como octal). Por iso na parte de abaixo falamos deles. Pero o código binario é fundamental como cultura algorítmica, por iso debemos estudialo. Traballando en binario aprendemos a codificar-decodificar, e iso desenvolve o pensamento algorítmico.
Os ordenadores son máquinas electrónicas, e como tales so teñen dous posibles estados: ou aceso ou apagado. Isto traducido a símbolos quere dicir.

0 apagado
1 aceso
Para contar números maiores terán que combinar estes dous díxitos. Fíxate en como combinas os números do 0 a 9 na codificación decimal (pasaches polo menos dous cursos de primaria aprendendo) e verás que na codificación binaria seguimos exactamente o mesmo proceso.
| Codificación decimal | Números cun so díxito | Codificación binaria |
|---|---|---|
|
0 |
No caso da codificación binaria, como só teño dous díxitos tan só podo representar dous números |
0 |
|
1 |
1 |
|
|
2 |
||
|
3 |
||
|
4 |
||
|
5 |
||
|
6 |
||
|
7 |
||
|
8 |
||
|
9 |
O seguinte número despois do 9 é poñer o número 1 e empezar a combinalos todos.
| Codificación | decimal | Números con dous díxitos | Codificación | binaria |
|---|---|---|---|---|
|
1 |
0 |
No caso da codificación binaria así so poderei obter dous números novos (fronte aos 90 que obteño en decimal) |
1 |
0 |
|
1 |
1 |
1 |
1 |
|
|
1 |
2 |
|||
|
1 |
3 |
|||
|
1 |
4 |
|||
|
1 |
5 |
|||
|
1 |
6 |
|||
|
1 |
7 |
|||
|
... |
... |
|||
|
9 |
9 |
Cando remato de facer todas as combinacións posibles terei que engadir un novo díxito:
| Codificación | decimal | Números con tres díxitos | Codificación | binaria | ||
|---|---|---|---|---|---|---|
|
1 |
0 |
0 |
Neste caso so teño catro combinacións en binario (fronte as 900 en decimal) |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
|
|
1 |
0 |
2 |
1 |
1 |
0 |
|
|
1 |
0 |
3 |
1 |
1 |
1 |
|
|
1 |
0 |
4 |
||||
|
1 |
0 |
5 |
||||
|
1 |
0 |
6 |
||||
|
1 |
0 |
7 |
||||
|
... |
... |
... |
||||
|
9 |
9 |
9 |
Reto:
Agora que sabes como construír o código binario, continuar non é difícil. Observa os quince primeiros números en decimal e en binario e atrévete a continuar:
|
Números decimais |
Números binarios |
||||
|---|---|---|---|---|---|
|
0 |
0 |
||||
|
1 |
1 |
||||
|
2 |
1 |
0 |
|||
|
3 |
1 |
1 |
|||
|
4 |
1 |
0 |
0 |
||
|
5 |
1 |
0 |
1 |
||
|
6 |
1 |
1 |
0 |
||
|
7 |
1 |
1 |
1 |
||
|
8 |
1 |
0 |
0 |
0 |
|
|
9 |
1 |
0 |
0 |
1 |
|
|
10 |
1 |
0 |
1 |
0 |
|
|
11 |
1 |
0 |
1 |
1 |
|
|
12 |
1 |
1 |
0 |
0 |
|
|
13 |
1 |
1 |
0 |
1 |
|
|
14 |
1 |
1 |
1 |
0 |
|
|
15 |
1 |
1 |
1 |
1 |
|
Co seguinte programa de Scratch poderás saber como se escribe calquera número decimal en codificación binaria:
[Scratch: Uso de funcións: binarizar]
Como contan os programadores (software)
O problema de almacenar eficientemente información
De entrada convén ter presente que moitos dos números que vemos nos ordenadores (procesador 32/64 bits, RAM 256 MB, Nintendo 64, Amstrand 128...) son potencia de 2, e calquera aspirante a programador terá que ter chapadas cando menos as 10 primeiras potencias:
| 20 = 1 | 21 = 2 | 22 = 4 | 23 = 8 | 24 = 16 | 25 = 32 | 26 = 64 | 27 = 128 | 28 = 256 | 29 = 512 | 210 = 1024 |
Truco para decodificar rápidamente de binario a decimal, por se te atopas un byte en binario:
- almacenas unha potencia de 2 a cada dedo e gardas a orde
- un número binario de tipo ABCD EFGH (todos os que vexas serán de 8 díxitos) é igual a A·28+B·27+... = A·256 + B·128+C·64+...
- Agora mentalmente vas sumando a potencia que tes almacenada en cada dedo cando o díxito binario sexa un 1
Doutra banda sabemos que o ordenador non utiliza bits (iso é o que fan os circuitos dixitais) senón bytes para almacenar información, sendo 1 byte = 8 bits. Os bytes veñen sendo as letras do ordenador que logo formarán palabras e frases.
Por que 8 bits se preguntan con razón moitos estudantes de informática?. Pois en realidade non é obrigatorio, e moi probablemente nun futuro próximo os bytes teñan 10 bits (senón é asi, sera por que utilicemos qbits, bits cuánticos).
O problema dos deseñadores de ordenadores consistía en poder almacenar os caracteres do alfabeto latino (en realidade só os do inglés) sen ocupar moito espazo de memoria. Como curiosidade decir que nunha primeria fase se utilizaron bytes de 7 bits que permiten almacenar 128 caracteres distintos (27 = 128). Como viron que iso quedaba escaso (por exemplo, non podía poñerse letras con tiles) optouse polos 8 bits, 28 = 256 caracteres distintos, cada un con un número binario de 8 dixitos. A isto é o que lle chamamos código ASCII, un sistema de codificación de caracteres que utiliza 8 bits por caracter e ten sido moito tempo o estándar de codificación. A día de hoxe está sendo substituido por outro sistema chamado UNICODE, pero moito profesorado aínda non se decatou. De todos xeitos coñecer ASCII é fundamental na Cultura Algorítmica.
Vexamos como escribimos distintos caracteres dependendo de se somos un ordenador ou un humano que ten unha táboa co seu lugar en ASCII, tendo en conta que temos 256 lugares:
| Caracter | Ordenador | Humano con táboa ASCII |
| 0 | 0011 0000 | 48 |
| A | 0100 0001 | 65 |
| a | 0110 0001 | 97 |
| p | 0111 0000 | 112 |
Se aprendiches a decodificar binario, vaste decatar que os números en binario son os valores decimais da posición na táboa ASCII. É decir, para gardar un '1' ningún ordenador escribe 00000001, o que fai é almacenar o lugar (en programación diremos índice) dese caracter humano na táboa de codificación, neste caso ASCII (o do 1 é o 49).
O problema de escribir eficientemente información
E un humano programador?. Pois un humano programador intenta compactar o máis posible a información. Por iso, determina que se utiliza código hexadecimal en vez de decimal para almacenar os lugares dos caracteres poderá aforrar 1/3 do espazo de escritura/almacenamento ( a cambio de amargar a moitos estudantes de Secundaria ;-)
O código hexadecimal (chamado HEX) utiliza 16 díxitos para a súas unidades, polo que podemos contar de 0 a 15 en decimal utilizando un único díxito:
| Díxitos hexadecimais | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Correspondencia decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Como se escriben os números con decenas hexadecimais?. Pois igual que en decimal, pero con decenas hexadecimais que valen 16. O número decimal 16 será 10 en HEX, o número 17 será 11...
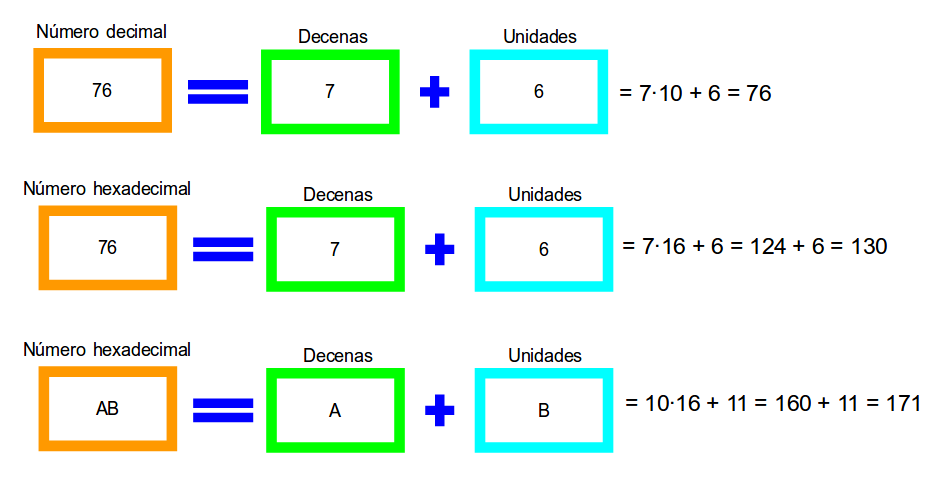
Número decimal maior que 10: AB = A decenas + B unidades = A·10 + B
Número hexadecimal maior que 15 en decimal: AB = A decenas hexadecimais + B unidades = A·16 + B
| Decimal | Hexadecimal |
| 10 | A |
| 16 | 10 |
| 20 = 1· 16+ 4 | 14 |
| 26 = 1 · 16 +10 | 1A |
| 31 = 1 · 16 + 15 | 1F |
| 32 = 2·16+ 0 | 20 |
| 100 = 6·16 + 4 | 64 |
O mesmo sería para centenas (ABC en hexadecimal sería A centenas hexadecimais + B decenas hexadecimais + C).
Exercicio:
1. Practica un pouco pasando de decimal a hexadecimal descompoñendo por tanteo en potencias de 16 como na táboa anterior :
| Decimal | Hexadecimal |
| 12 = | |
| 64 = | |
| 127= | |
| 129= | |
| 200= | |
| 255= |
2. E viveceversa, de hexadecimal a decimal: #0F, #F1, #7B, #AA, #FF
| Hexadecimal | Decimal |
| 0F | |
| F1 | |
| 7B | |
| AA | |
| FF |
E agora ven a razón de peso para escribir en hexadecimal. Se te fixas cando chegamos ao 100 en decimal necesitamos 3 dixitos decimais pero só 2 hexadecimais (100 é 64). Isto vai ser así ata o 255 (FF en hexadecimal; o 256 será 100 en hexadecimal). E que ten o rango 0-255?. Pois que son 28 valores distintos, que son casualmente o número de caracteres distintos que podemos almancenar nun byte.
Conclusión: os humanos programadores optan por contar en hexadecimal por que poden escribir 256 lugares distintos dunha táboa utilizando 2 dixitos en vez de 3 (isto é un aforro do 33%).
| Caracter | Ordenador (binario) | Humano con táboa (decimal) | Humano programador con táboa (HEX) |
| 0 | 0011 0000 | 48 | 30 |
| A | 0100 0001 | 61 | 41 |
| a | 0110 0001 | 97 | 61 |
| p | 0111 0000 | 112 | 70 |
| { | 0111 1011 | 123 | 7B |
Onde atoparás os números hexadecimais?. En programación por todas parte, para codificar valores.
Por exemplo as cores que utilizamos no ordenador está codificadas en hexadecimal. Cada cor da pantalla é a suma de Vermello(Red), Verde(Green) e Azul (Blue) e a isto lle chamamos modo RGB. Cada unha destas cores utiliza 8 bits/píxel para gardar a súa tonalidade, polo que temos 28 = 256 cores vermellas diferentes, 256 verdes e 256 azuis. Cada cor de cada píxel utiliza 8+8+8 bits = 24 bits/píxel e temos 256·256·256 = 224 cores distintas (a isto logo que habería que sumarlle a transparencia, que serán 8 bits máis).
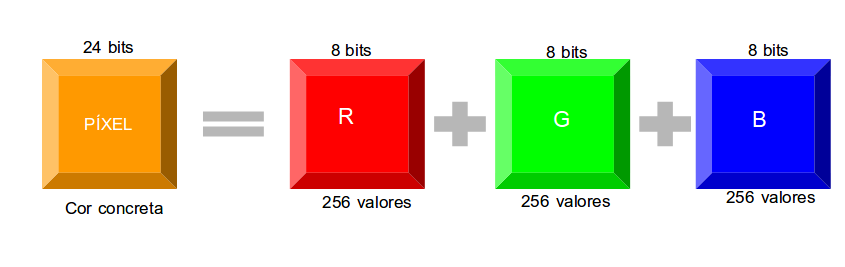
Para decirlle ao ordenador que cor queremos poderíamos escribilo en decimal: Cor = (R,G,B). Por exemplo un vermello puro sería (255,0,0) e un azul (0,0,255), Pero os programas o entenden con números hexadecimais e de un xeito compacto: Cor = #RGB (o símbolo # é para indicar un número). Entón teremos vermello = #FF0000 e azul = #0000FF.
![]()
Para programar HTML ou Python en modo gráfico (co uso de Bibliotecas como TkInter) é interesante poder ler/escribir o código hexadecimal, por exemplo para indicar unha cor concreta das 224 que temos á nosa disposición.
Vexamos como usa HTML o código hexadecimal. Escribamos unha palabra que teña unha cor e leamos o seu código:
| Palabra e cor escollida | Código HTML | Notación hexadecimal da cor |
| Vermello puro | <span style="color:#FF0000">Vermello</span> | #FF000 |
| Verde medio | <span style="color:#008000">Verde</span> | #008000 |
| Azul | <span style="color:#0000FF">Azul</span> | #0000FF |
| Amarelo | <span style="color:#FFFF00">Amarelo</span> | #FFFF00 |
| Gris | <span style="color:#808080">Gris</span> | #808080 |
En moitas páxinas e aplicacións tes a posibilidade de consultar unha cor polo seu código hexadecimal. Por exemplo en ColorCodes escolles cores premendo nelas, e obtés o código HEX, o decimal e outros:
Isto tamén podes facelo en Gimp e outros programas de manipulación gráfica.
E viceversa, tendo píxeles dunha cor podemos obter o seu código para utilizar esa cor noutro lado. A maioría dos programas teñen unha icona de contagotas para "roubar" cores, Se tes un navegador Firefox dende menú tes unha opción, Eyedropper, que fai isto en calquera páxina web.
Exercicio:
3. Cal sería o valor decimal da codificación das cores R G e B ?. E do verde medio?
4. No logo de AlgoRitmia temos 3 cores. Averigua o seu código HEX (tamén pode chamarse código html). Se es intelixente e estás a utilizar Firefox podes facelo directamente coa ferramenta Eyedropper.
Máis de almacenar información eficazmente: Bit, byte, nibble
Aínda que pensemos que nós escribimos os números en decimal ou en hexadecimal e logo temos un programa ou algoritmo para convertilo a binario (de aí que cando estudamos programación fagamos sempre algoritmos de binzarizar un decimal, por exemplo) non é a forma directa de codificar a información, temos un método máis eficaz chamado BCD (Binary-Coded Decimal) que usa a metade dun byte, catro bits, un nibble (estes nomes de bit - byte - nibble teñen un referente gastronómico en inglés, sendo nibble peniscar).
É decir, se temos o número 112 en decimal podemos convertilo a binario polo método estudado e teremos 112 = 64 + 32 + 16 = 0111 0000, pero isto non é o que vai ler o hardware. O número 112 aplicando o método BCD será 1|1| 2 e cada un deles en binario: 0001 0001 0010. Como ves agora usamos 12 dixitos contra 8, algo haberá que compense facelo así. Pois si, a razón é de sinxaleza ao ler e escribir. Vexamos como facelo con un número longo, 59237:
| Decimal | 5 | 9 | 2 | 3 | 7 |
| Binario BCD | 0101 | 1001 | 0010 | 0011 | 0111 |
A inmensa ventaxa é que non temos que facer operacións, só temos que saber escribir en binario dende 0 ata 9.
Para pasar de hexadecimal a binario é o mesmo, pero máis sinxelo, collemos cada díxito hexadecimal e escribimos o seu equivalente en binario. É aquí onde se entende mellor a razón do uso de BCD: cada díxito binario pode representarse con un nibble único (temos 24 = 16 combinacións con 4 bits, e tamén 16 díxitos hexadecimais)
Por exemplo, #AB sería #1010 1011. Vexamos con un número grande, #59017 que en decimal sería 364807, e se tivesemos que binarizar levaría varías operacións:
| Hexadecimal | 5 | 9 | 0 | 1 | 7 |
| Binario BCD | 0101 | 1001 | 0000 | 0001 | 0111 |
Como contan os ordenadores e os programadores Asignar valores As catro reglas
As comparacións son odiosas A lóxica dos ordenadores Eu concateno, ti concatenas, el concatena... Pase primerio, por favor