Pedra_papel_tesoira

Pedra_papel_tesoira é, xunto co O Aforcado, o xogo máis probable que debe programar alguén que estea aprendendo. A raźon é, ademais de que todo o mundo o coñece (existe ata un campionato mundial, por se tiñas dúbidas ;-), a súa estrutura algorítmica, moi sinxela de inicio pero que pode programarse a distintos niveis (con gráficos ou sen eles, 2 xogadores ou contra o ordenador, ao chou ou con "intelixencia artificial"...).

Pode aportar algo xogalo antes de saber programar?. Sen dúbida, é un xogo que axuda a familiarizarse dende moi pequenos coas estruturas condicionais. Outra variante en clase que ademais permite practicar cálculo sería o xogo clásico dos CHINOS (o nome é referente ás chinas, pedras pequenas, non aos chineses). Vexamos distintas posibilidades:

Versión 1: Xogo tradicional

Non hai moito que dicir. É interesante como recurso de clase (podes xogar en calquera momento) e poden facerse rapidamente campionatos. O noso obxectivo debe ser cambiar as estratexias de "azar" (en realidade o noso cerebro é incapaz de xogar ao chou, pero preferimos enganarnos ao respecto) por estratexias razoadas.

A partir de certas idades (Secundaria?) debe pedirse reflexionar sobre as estratexias exitosas depois de xogar a partida. Para iso pode haber unha terceira persoa que anote as xogadas e logo se revisen, comentando cales foron boas e malas decisións, aínda que a percepción (incorrecta, insistimos) de moitos xogadores é que o fan ao chou. Unha vez xogado bastante e revisadas as estratexias pode comentarse o que di un estudo sobre as mellores decisións:

• Empeza xogando papel porque hai máis probabilidades de que o contrincante empeze por pedra (con nenos pequenos seguramente non vale, tenderán a xogar a tesoira por ser a última palabra).
• Cando gañamos tendemos a repetir xogada (pero non máis de 3 veces). Sabendo isto podemos tomar unha decisión cando perdamos.
• Cando perdemos tendemos a cambiar a xogada. O mesmo.

Por suposto isto vale se non o sabe o noso adversario, e en todo caso ten unha validez estatística.

Versión 2: Diagrama de árbore

Nesta modalidade podemos facer dúas cousas:

• Crear un diagrama de árbore coas posibles combinacións, que na partida real axude a tomar unha decisión razoada en vez de ao chou (se na anterior partida escolliches pedra e perdiches e na anterior tesoira e empataches. Que deberías xogar agora?). Parece perder o tempo, pero axuda a razoar unha estratexia.

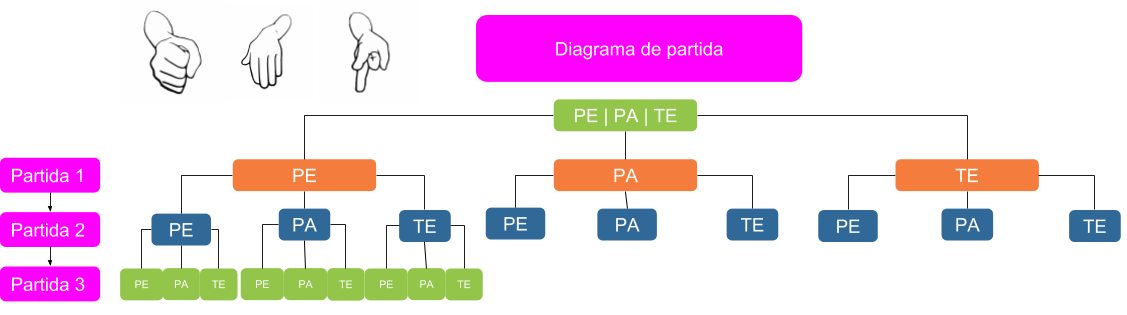
• Simular un xogo de 1 xogador creando un diagrama dunha partida e razoando a decisión seguinte (se escollo pedra e o meu opoñente tesoira, que debo facer na seguinte partida?).

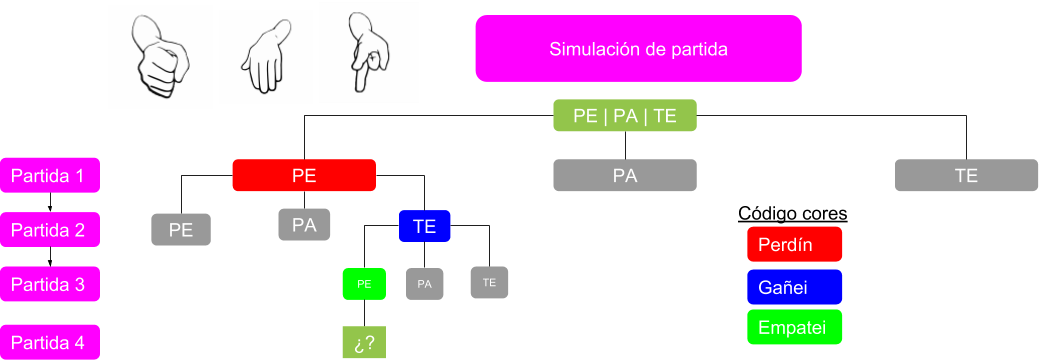
Con este diagrama poden poñerse varias partidas simuladas e analizar a estratexia seguida polos xogadores.

As dúas cousas axudan a explicitar unha estratexia, e de paso familiarizarnos cunha ferramenta básica da programación ( e doutros ámbitos coma xestión de recursos administrativos): o diagrama de decisións en árbore. Estamos anticipando algo que serán os datos estruturados non lineais, que non serán sinxelos de programar, pero que teñen unha importancia capital en grande cantidade de algoritmos reais, como, por exemplo, nos de Machine Learning e IA.

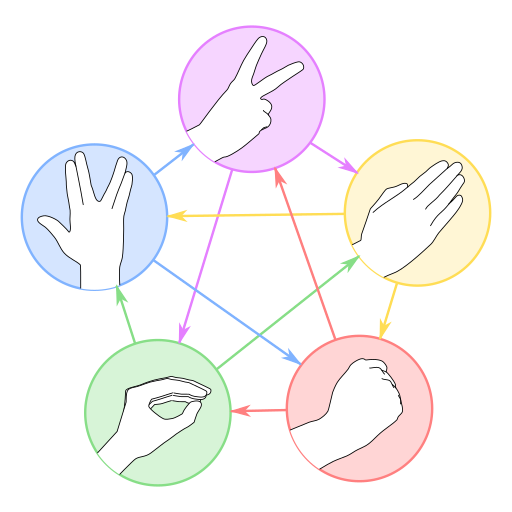
Versión 3: Pedra_papel_tesoira_lagarto_spock

Case que todo o alumnado e parte do profesorado coñecerá esta versión mellorada que aparece na famosa (e excesivamente alongada) serie Big Bang Theory.

Para alumnado que xa teña xogado ao xogo clásico pode ser unha boa idea aumentar a complexidade. Neste caso temos 5 posible signos, e as súas interacións pasan a ser 11 (se temos en conta o empate) en vez de 4:

 

Anexo: Para programar PEDRA_PAPEL_TESOIRA

Programar este xogo a nivel básico é sinxelo, e é un bó exercicio de escritura algorítmica en calquera linguaxe de programación ou en pseudocódigo. Se xa sabemos unha linguaxe como Scratch podemos probar a programalo cos seguinte niveis de dificultade algorítmica:

Nivel	Descrición
1	Partida simple ordenador-humano. O ordenador xoga ao chou.
2	Partida ao mellor de 3 puntos ordenador-humano. Ordenador xoga a chou.
3	Partida ao mellor de N puntos ordenador-humano. Alternativa: 2 xogadores humanos con teclas distintas.
4	Partida ao mellor de N puntos con intelixencia artificial: o ordenador aplica unha estratexia determinada no seu programa en función do resultado das partidas anteriores.

Curiosamente a mellor estratexia posible é xogar completamente ao chou. Isto pode facelo un ordenador pero non un humano (vale, sempre podemos coller un dado ;-)

Cubo de Rubik Moon 1110011 Pedra_papel_tesoira Robodrez Xogo da vida