Como xa comentabamos na definición de recursividade non sempre é mellor un proceso recursivo que un iterativo, vai depender do problema concreto. A solución será a mesma pero dende o punto de vista funcional da computación pode haber moita diferencia.
Cando recurrir é peor que iterar
O código recursivo da serie de Fibonacci visto no exemplo resolto é moi elegante e compacto, pero moi pouco eficiente dende un punto de vista computacional, en especial se temos que calcular números grandes:

Que sucede ao executar o programa?.
Pois que estamos a chamar a función dúas veces en cada chamada recursiva. Por exemplo, para calcular fib(5) temos que calcular fib(4) e fib(3), pero logo en fib(4) voltamos a calcular fib(3). Isto é pouco eficaz. Vexamos isto counha árbore:
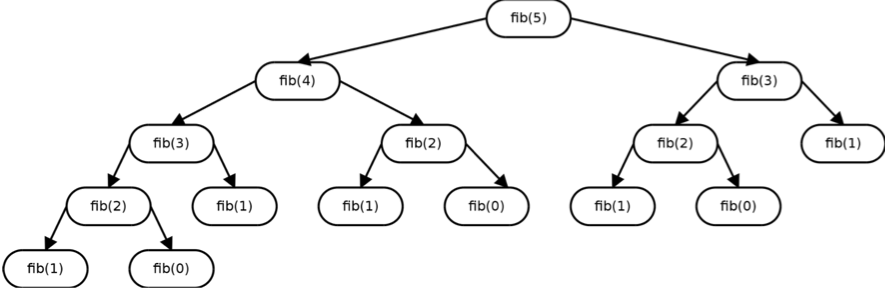
Para calcular o termo 5 facemos 15 ramificacións, o cal será un nº estratosférico en caso de números máis grandes.
Neste caso a solución mediante iteración será menos elegante, pero máis óptima computacionalmente falando. Vexamos un par de exemplos posibles:
[Repl.it: Fibonacci sen recursividade]
Cantas veces repetimos o bucle?. Pois para calcular un número n, iteramos n-1 veces. Isto é moitísimo menos que no caso recursivo. Entón non aplico a recursividade? Pois non, depende do problema e dos métodos que teñamos para resolvelos. Como norma xeral a recursividade dará un código máis elegante e compacto, polo tanto fácil de ler (outra cousa é entendelo ;-), pero menos eficiente. Por exemplo un código para percorrer todos os cartafoles do ordenador buscando un ficheiro concreto seguro que utiliza un código recursivo, pois o programadado non coñece de antemán a estrura completa de cartafoles. Existe toda unha chea de problemas que poden abordarxe con unha metodoloxía recursiva para optimizalos. Algúns deles están incluidos na técnica "Divide e vencerás" e outros na de Volta Atrás (Backtracking).